Ensemble Models

Ensemble is the art of combining diverse set of learners (Individual models) together to improvise on the stability and predictive power of the model. Roughly, ensemble learning methods, that often trust the top rankings of many machine learning competitions are based on the hypothesis that combining multiple models together can often produce a much more powerful model. Ensemble learning is a machine learning paradigm where multiple models (often called “weak learners”) are trained to solve the same problem and combined to get better results. Click for more info.

Most of the time (including in the well-known bagging and boosting methods) a single base learning algorithm is used so that we have homogeneous weak learners that are trained in different ways. The ensemble model we obtain is then said to be “homogeneous”. However, there also exist some methods that use different type of base learning algorithms: some heterogeneous weak learners are then combined into an “heterogeneous ensembles model”.

One important point is that our choice of weak learners should be coherent with the way we aggregate these models. If we choose base models with low bias but high variance, it should be with an aggregating method that tends to reduce variance whereas if we choose base models with low variance but high bias, it should be with an aggregating method that tends to reduce bias.

Bagging, Boosting, and Stacking

Ensemble learning has many types but the three more popular ensemble learning techniques are mentioned below:

• Bagging
• Boosting
• Stacking

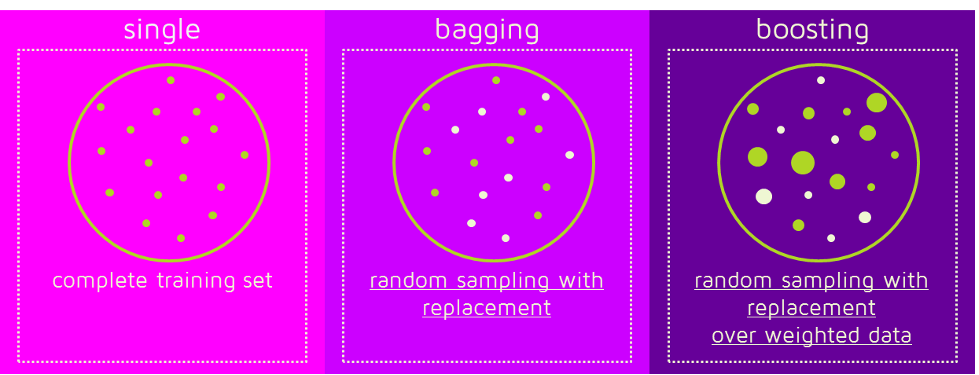
Bagging

bagging, often considers homogeneous weak learners, learns them independently from each other in parallel and combines them following some kind of deterministic averaging process. Very roughly, we can say that bagging will mainly focus at getting an ensemble model with less variance than its components. Bagging tries to implement similar learners on small sample populations and then takes a mean of all the predictions. In generalized bagging, you can use different learners on different population. As you expect this helps us to reduce the variance error.

Boosting

boosting, that often considers homogeneous weak learners, learns them sequentially in a very adaptative way (a base model depends on the previous ones) and combines them following a deterministic strategy. Very roughly, boosting and stacking will mainly try to produce strong models less biased than their components (even if variance can also be reduced). Boosting is an iterative technique which adjust the weight of an observation based on the last classification. If an observation was classified incorrectly, it tries to increase the weight of this observation and vice versa. Boosting in general decreases the bias error and builds strong predictive models. However, they may overfit on the training data.

The technique of Boosting uses various loss functions. In case of Adaptive Boosting or AdaBoost, it minimizes the exponential loss function that can make the algorithm sensitive to the outliers. With Gradient Boosting, any differentiable loss function can be utilized. Gradient

Boosting algorithm is more robust to outliers than AdaBoost. (Ref)

The success of statistical boosting algorithms can be summarized as:

• The ability of the boosting algorithms to incorporate automated variable selection and model choice in the fitting process,
• The flexibility regarding the type of predictor effects that can be included in the final model,
• The stability of these algorithms in high-dimensional data with several candidate variables rather than observations, a setting where most conventional estimation algorithms for regression settings collapse

Two important boosting algorithms are AdaBoost (Adaptive Boosting) and Gradient Boosting.

Stacking

Stacking: that often considers heterogeneous weak learners, learns them in parallel and combines them by training a meta-model to output a prediction based on the different weak models’ predictions

AdaBoost & Gradient Boosting

These two algorithms are variants of boosting algorithms.

Adaptative boosting

AdaBoost or Adaptive Boosting is the first Boosting ensemble model. The method automatically adjusts its parameters to the data based on the actual performance in the current iteration. Meaning, both the weights for re-weighting the data and the weights for the final aggregation are re-computed iteratively.

AdaBoost tries to boost the performance of a simple base-learner by iteratively shifting the focus towards problematic observations that are challenging to predict. In AdaBoost, this shifting is done by up-weighting observations that were misclassified before.

In adaptative boosting (often called “adaboost”), we try to define our ensemble model as a weighted sum of L weak learners. Finding the best ensemble model with this form is a difficult optimization problem. Then, instead of trying to solve it in one single shot (finding all the coefficients and weak learners that give the best overall additive model), we make use of an iterative optimization process that is much more tractable, even if it can lead to a sub-optimal solution. More especially, we add the weak learners one by one, looking at each iteration for the best possible pair (coefficient, weak learner) to add to the current ensemble model.

AdaBoost was the first really successful boosting algorithm developed for binary classification. It is the best starting point for understanding boosting.

Modern boosting methods build on AdaBoost, most notably stochastic gradient boosting machines.

In Adaptive Boosting or AdaBoost, the loss function which we try to minimize is an exponential loss function that can make the algorithm sensitive to the outliers.

In AdaBoost, the shortcomings of the existing weak learners can be identified by high-weight data points.

AdaBoost is mainly used for classification, however since it is a meta-algorithm (which means it can be used together with other algorithms for performance improvement, including regression tasks. For example, Scikit-Learn, has an implementation of an Adaboost regressor. In the documentation for such regressor, the developers mention that: An AdaBoost regressor is a meta-estimator that begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction. As such, subsequent regressors focus more on difficult cases.

Gradient Boosting

Gradient boosting is an approach where new models are created that predict the residuals or errors of prior models and then added together to make the final prediction. It is called gradient boosting because it uses a gradient descent algorithm to minimize the loss when adding new models. (Ref)

Gradient boosting tries to boost the performance of a simple base-learner by iteratively shifting the focus towards problematic observations that are challenging to predict. In Gradient boosting, this shifting is done by identifying the difficult observations by large residuals computed in the previous iterations.

Gradient Boost is a robust machine learning algorithm made up of Gradient descent and Boosting. The word ‘gradient’ implies that you can have two or more derivatives of the same function.

The technique yields a direct interpretation of boosting methods from the perspective of numerical optimization in a function space and generalizes them by allowing optimization of an arbitrary loss function.

The loss function is gradient boosting can be any differentiable loss function, and so Gradient Boosting algorithm is more robust to outliers than AdaBoost. (recall that the AdaBoost uses exponential loss function which can be sensitive to the outliers. Gradient boosting can use different loss functions, and hence is less prone to the outliers).

Gradient Boosting has three main components: additive model, loss function and a weak learner.

This approach supports both regression and classification predictive modeling problems.

In Gradient Boosting, the shortcomings of the existing weak learners can be identified by gradients.