Item-Item Collaborative Filtering
Published:
Collaborative filtering is considered to be the most popular and widely implemented technique in Recommender Systems.
Here we implement a Item-Item Collaborative Filtering model for movie recommendation using the MovieLens dataset on Kaggle. Note that you need to put the original data of the ratings, named rating.csv and save it to the directory Data.
Here we briefly talk about the code and results, and then dive a little bit into the theory of the User-User Collaborative filtering models.
### Codes & Results
The code consist of two parts. One is for the data preprocessing, and one implements and tests the User-User Collaborative Filtering.
- The data preprocessing code: It has two main jobs:
- it decreases the size of the data: The original data contains the records for 20 million ratings, which requires a lot of computations. This is specially problomatic if we do not use parallel computations. To allow us to run this code on a pc, we shrink the data to contain only those users that are the among the most common users. Similarly, we filter the data to include only the most common movies. The filtered version of the data, titled small_rating.csv is then saved to the directory Data.
- It extracts the useful information from the small_rating.csv and save it in some dictionaries in the directory Data. We are going to use these dictionaries to implement the User-User collaborative filtering.
- The Item-Item Collaborative Filtering: This file implements the User-User Collaborative Filtering.
We use 80% of the data (i.e. small_rating.csv) for training and the remaining for the testing. The MSE errors for the training and testing are as follows:
MSE for train set = 0.519016025752116
MSE for test set = 0.5454512099616208
Note that to get a sense of whether this is a good performance or not we need to compare it with a benchmark, which I do not get into the details in here, but one simple case can be to for each user output his/her average rating as the prediction for a new movie. Another important factor is to note that this MSE is for a subset of the data that has most common users and most common movies. If we performe this algorithm on the original data (20 million ratings), it would take considerably longer time to finish the computations, and the error would increase as well for both the train and test set.
### Theory of Item-Item Collaborative Filtering
Here the goal is to design a model that predicts the ratings that an item would get from a user that does not have interaction with it before (i.e. unseen product). This is practically a regression problem, and the approach we are taking here, i.e. item-item collaborative filtering is basically building a regression model with few extra steps.
The algorithm for the item-item collaborative filtering is summarized in the following:
# Item-Item Collaborative Filtering
# for predicting the rating that item i would get from user u:
#-------------------------------------------------------
1. For each item j != i:
If they have minimum number of common users:
Calculate the Similarity Weight between item j and item i
2. Keep only the top neighboring items (There are different techniques for doing this)
3. Calculate the linear average of the normalized ratings that the (top neighboring) items receive, and the weights of this linear function are the similarity weights. We also add back the off-set term of the normalization for item i back to the rating.
Note that if we have N users and M movies, when training, we need to: for each item, look at all other item, and, calculate the similarity between the two items (i.e. its a mathematical operation which includes vectors of length #users). Hence the computational time of this algorithm during the training process is $O(N×M^2 )$, and since we usually $N \gg M$, the running time of this algorithm is better than the User-User Collaborative Filtering Algorithm, which has a running time of $O(M×N^2 )$.
Another common problem is that there may be differences in the items’ individual rating scales. In other words, different brands may receive different rating values from users for the same level of quality/releavabce. For example, domestic products might get (on average) higher ratings that the similar exotic products.
To solve this problem, we normalize the rating by centering them (i.e. subtracting the average ratings that an item receives). This technique is called mean-centering.
Score
The score is calculated as:
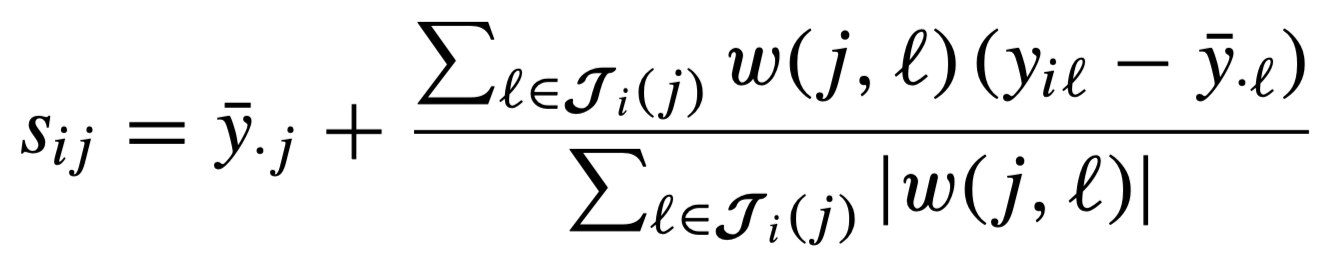
where the weights are the Pearson Correlation (PC) similarity metric. We note that other similarity metrics such as Cosine Ssimilarity, Mean Squared Difference and Spearman Rank Correlation Coefficient. For more info, see Chapter 2 of [1] and [2].
The neighborhood selection also takes a similar procedure as that of the Item-Item CF. For more info, see User-User CF project.
To see the Github repository for this project, see Github.
