Finding Control Policy for Mountain Car using TD(n) for finding the Q-value Function Approximator

A car is on a one-dimensional track, positioned between two “mountains”. The goal is to drive up the mountain on the right; however, the car’s engine is not strong enough to scale the mountain in a single pass. Therefore, the only way to succeed is to drive back and forth to build up momentum.

The car’s state, at any point in time, is given by a two-dimensional vector containing its horizonal position and velocity. The car commences each episode stationary, at the bottom of the valley between the hills (at position approximately -0.5), and the episode ends when either the car reaches the flag (position > 0.5).

At each move, the car has three actions available to it: push left, push right or do nothing, and a penalty of 1 unit is applied for each move taken (including doing nothing). This actually allows for using the exploration technique called optimistic initial values.

The steps of this code is summarized in the following flowchart.

1. Create RBF kernels (each one with different $\sigma$), train them on some samples initially. These kernels are used to create new features.
2. We then build three different linear regression models (each for a different action) for the state-action values (Q-values).
3. We initialize all the state-action values to 0. This is optimistic intitial values. This means that even if we do not use $\epsilon$-greedy, but use the pure greedy action selection, these optimistic intitial values results in automatic explorations.
4. At each step of the training, sample from the envirmonment, use TD(n) to update the Q-values, and use greedy or $\epsilon$-greedy action selection. Continue until converge or until the stopping criteria is met.
5. The greedy algorithm applied to the final Q-values is the optimal policy

We also record (a video for) the performance of the algorithm for the optimal policy.

After training the model, the results are shown as the follows:

The performance of the optimal policy:

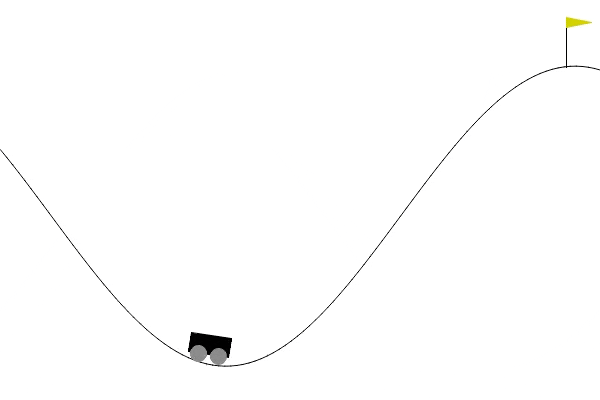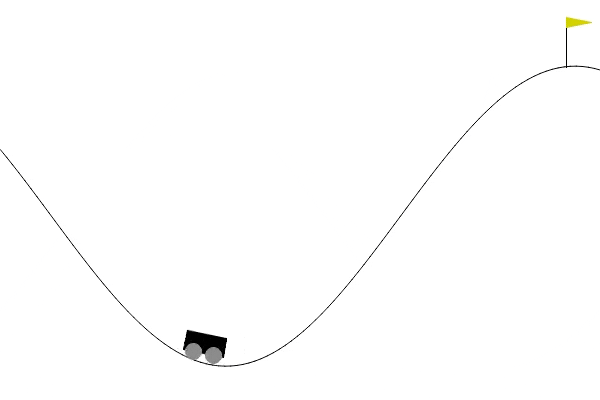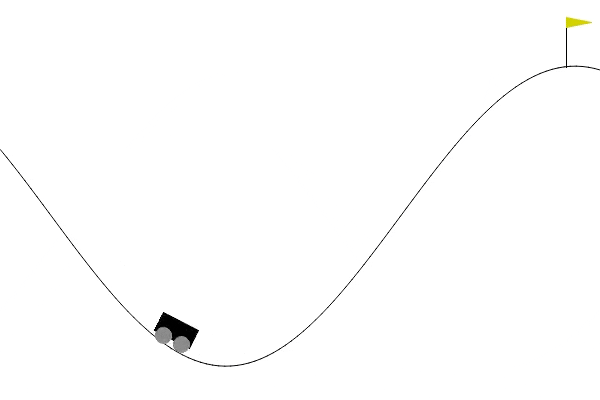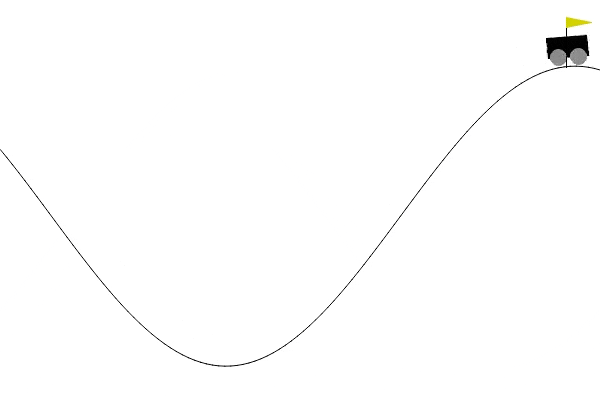
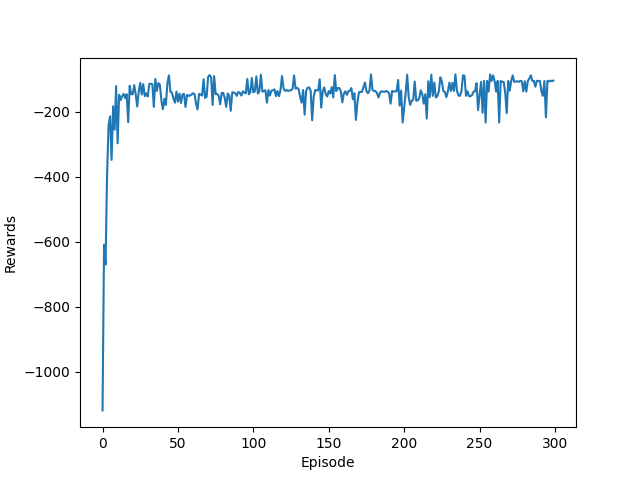
Average total reward over different episodes:

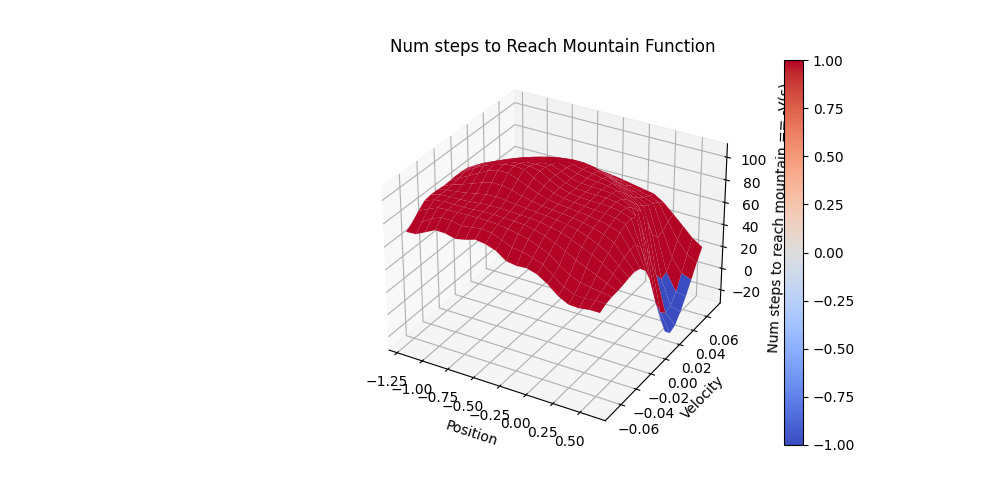
And the average # steps to reach to the top of the mountain at different state-action pairs (which is practically $(-Q^*(s,a))$) is shown in the following figure:

To see the Github repository for this project, see Github.