Policy Gradient with Baseline
Published:
Polciy gradient approaches aim at directly modeling the policy and trying to optimize it. There are few challenges for this approach:
What would be the objective function to train the policy? The answer is shown in the following figure:
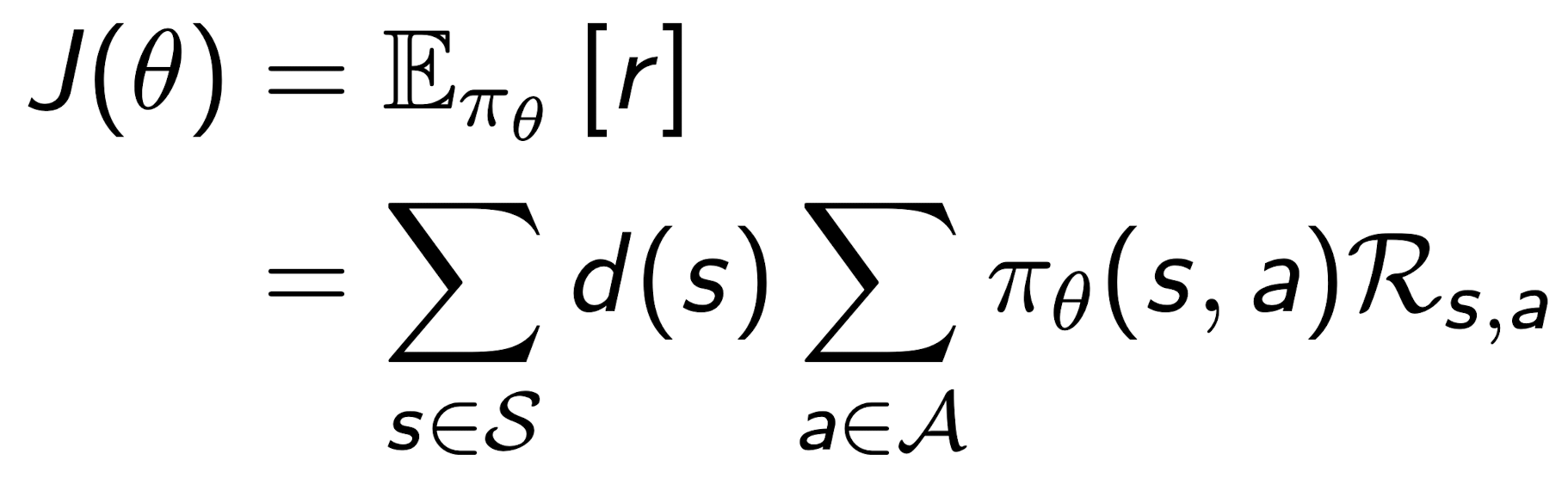
There are more details on how we arrive at this objective function for training the policy function approximator. I recommend reading the [1], [2] and [3] for more information on this.
How to manually calculate the gradient? This is an implementation challenge, rather than a theoretical one. If, for instance, we use neural networks as the function approximator, then calculating the gradient of the objective funciton w.r.t. the weights could be troublesome. There is an interesting trick that we can use to do this. We can use the automatic differentiation provided in Tensorflow. The trick is to use only operations that keras “knows about” aka that exist as operations in TensorFlow, and the TensorFlow will automatically a graph of operations to backpropagate against. Now, in order to do this, we manually implement a hidden layer in the code, and the fully connected neural network that we are using for the policy gradient is created by adding one layer after another. This allows TensorFlow to do automatic differentiation.
This approach results in high variance. There is a technique called “baseline” for which we use the state value functions V(s) to decrease the variance of the model. This requires a value function approximator (here we use another neural network) to estimate the state-value functions.
Results
We apply this method to the Cart Pole environment. The results is shown in the following figure:
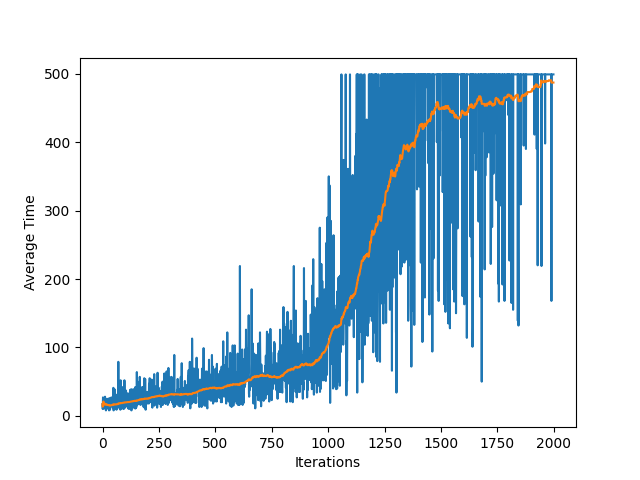
We also record (a video for) the performance of the algorithm for the optimal policy.
To see the Github repository for this project, see Github.
