Simulating Pandemics with Multiple Waves

The evolves as follows: Individuals in the pool of Susceptibles contact the infectious individuals and become exposed. The exposed individuals after certain period become infectious, and the infectious individuals will be removed after certain period. This is the essence of the SEIR epidemiological model.

Now we can see that there is no room for the effect of the behavior of the individuals in the society on how the disease spreads. For example, we expect that with higher number of infectious individuals in the society people tend to practice the safety guidelines more, and hence the speed of the spread of the disease decrease. To incorporate such behaviors, we use a model called replicator-dynamics model to capture the behavior of the individuals in the society. The replicator dynamics model divides the sociey into two group: those who follow the safety guidelines, which their ratio is $x$, and the class of individuals who does not follow the safety guidelines, which their ratio is $1-x$. Then there is a competition between these two classes, and the payoff of following each class is given in a payoff matrix.

To couple these two models together, we assume (intuitively) that the disease transmission rate depends on the how many individuals do not follow the safety guidelines. And the payoff matrix in the replicator-dynamics changes with the change in the number of infectious individuals. This gives a complete picture of the pandemic, as shown in the following figure.

Now we can see whether our proposed model can capture multiple waves of the disease or not. As shown in the following figure, the proposed model is well-suited for the pandemics with multiple waves of the disease.

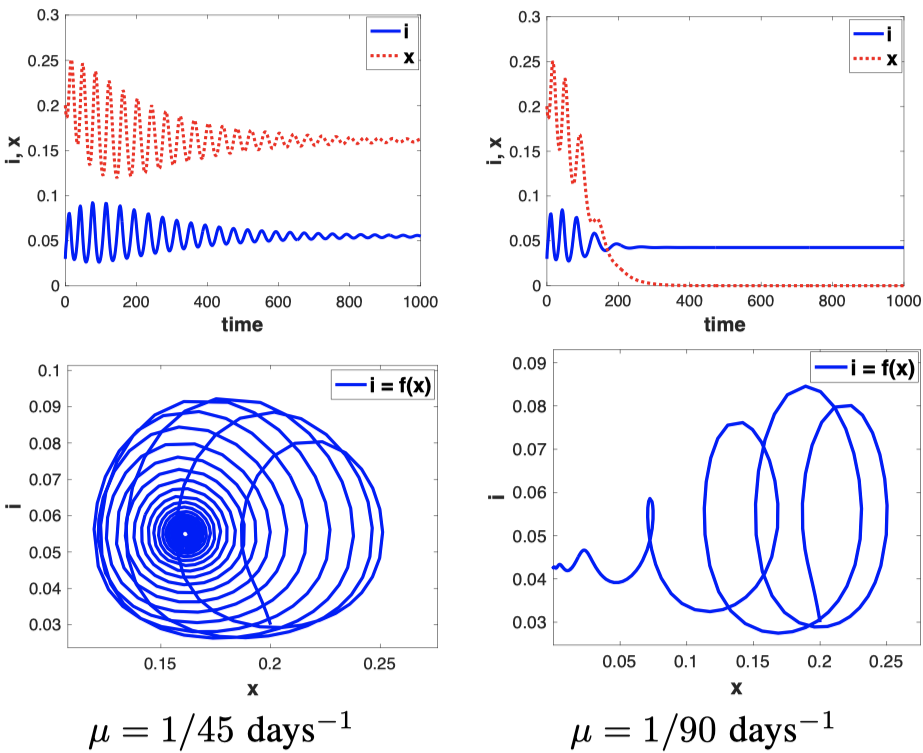
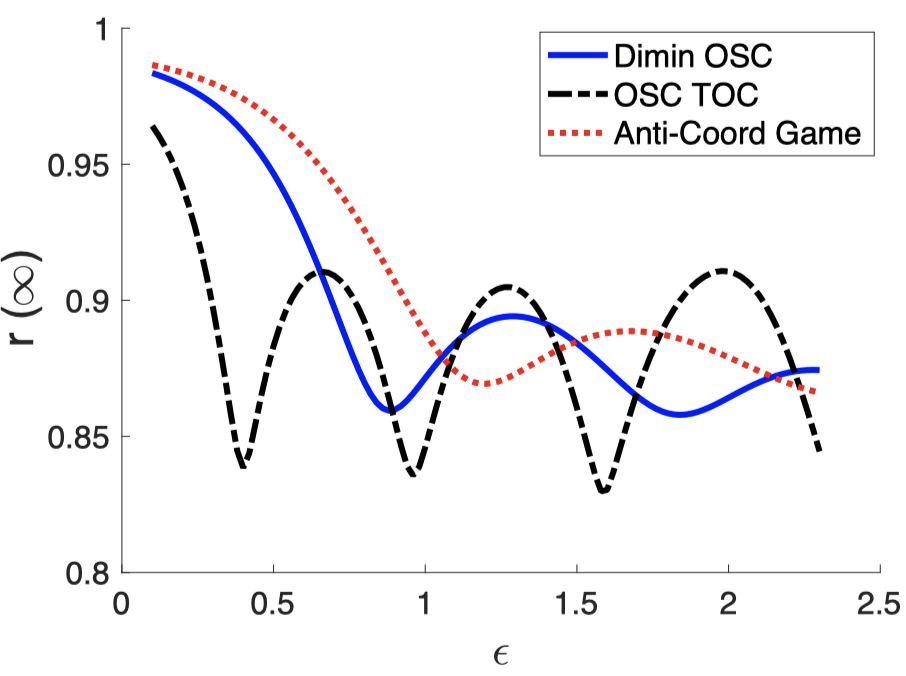
And let’s see if the proposed model can capture the eventual number of the removed individuals. Note that we always have a small number of infecious individuals existent in the society (similar to Influenza)

The pdf file for the corresponding publication for this project can be found in link. The Github repository for this project can be found in Github.